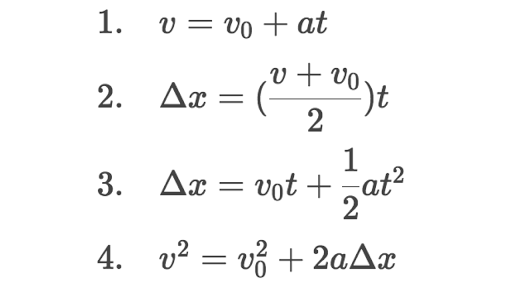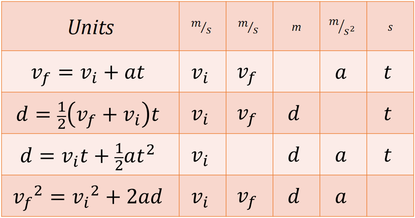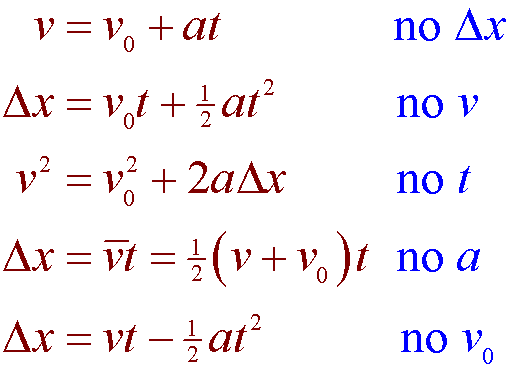Perfect 2nd Kinematic Equation

Learn how to derive the second equation of motion in Kinematics.

2nd kinematic equation. Unlike the first and second equations of motion there is no obvious way to derive the third equation of motion the one that relates velocity to position using calculus. The variables include acceleration a time t displacement d final velocity vf and initial velocity vi. This equation is given by the relation.

Solves for the kinematic equations based on the inputs you entered. Uniform acceleration This is the equation of the line of the velocity vs time graph when an object is undergoing uniform acceleration. 5 Draw the free body diagram for the red mass when it is accelerating upward.

There are only two forces and both are vertical. 4 Using the second kinematic equation d vot 12at2 and assuming an initial velocity of zero solve for acceleration a. The truck attains the final velocity of 35 ms in.

According to Newtons second law equation F net m v u t 12 1 v 6 15 v 6 12 15 v 6 180 v 180 6 v 186 ms Therefore after 15 seconds the speed of the rubber tyre will be 186 ms. Draw FBD including forces on the lab report. Each equation contains four variables.

The remainder of the slides is problem solving that combines Newtons Second Law and the kinematic equations in a single problem. F m a Acceleration is simply the rate at which the velocity of an object changes with time. Kinematic equations relate the variables of motion to one another.

This gives us the position-time equation for constant acceleration also known as the second equation of motion. The second and third slides are reminders on the concept of weight and Fmg. Displacement of the object.